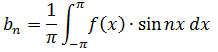■　「フーリエ変換」に関する知識を学ぶ！

　

普段の生活には全く縁がないと思われる数学知識ですが、市場分析という

世界に足を踏み入れたのであれば無関係とは言えない知識になるでしょう。

　

　

参考書買っても中身がさっぱり理解できない・・　(ﾉ_･｡)

あ～どうやって理解したらいいのかなぁ・・

諦めよっかなぁ・・

　

　

と知識の取得を諦めてしまう方も多いことでしょう。当コンテンツは、そんな方々

へお贈りいたします。

　　

　

　

■　今回扱う知識は「フーリエ級数を改めて理解する②」

　

　

【常に過去の記事内容を把握！】　

当ブログにおけるフーリエ変換の解説はExcelで体験したフーリエ変換にて出力

された値を再現していく方式で解説していきます。

よってExcelの分析ツールによるフーリエ変換が行えるようにしておいてください。

解説には時間がかかるのでExcelの分析ツールでフーリエ変換を繰り返して使い

方を慣れておくと良いかもしれませんね　(^-^)/

一応、過去の記事へのリンクを載せておきます！

　

　

参考　：　知識０でフーリエ変換をしてみる

参考　：　フーリエ変換とは何に変換されるのか？

参考　：　逆フーリエ変換にて各領域を行き来する

参考　：　フーリエ変換と周波数成分

参考　：　フーリエ級数から理解していく

参考　：　フーリエ級数と直交

参考　：　フーリエ級数と偶・奇関数

参考　：　【超重要】波の基礎知識

参考　：　ある関数とフーリエ級数

参考　：　フーリエ級数の係数　a0　を求める

参考　：　フーリエ級数の係数an・bn　を求める

参考　：　複素フーリエ級数の導出　その1

参考　：　複素フーリエ級数の導出　その2

参考　：　複素フーリエ級数の係数を求める

参考　：　フーリエ級数を改めて理解する①

　

　

　

　

　

　

【係数を操作して自由自在な波を作る】

前回は改めてフーリエ級数を理解する内容でした。具体的には、Sin波とCos波

は異なる周波数同士で合成すると、元のSin波とCos波とは異なる波形になると

いうことでした。

では、今回は係数　an　bn　の値を変化させることで自由自在な波形が作れる

ということについて解説します。

　

　

　

　

　

【パラメータである係数を操作する】

フーリエ級数の数式を改めて観察しましょう。

　

　

　

　

Sin・Cosの前に　an　bn　という係数がありますよね？実は、その係数を操作する

ことで簡単に上図以外の波形にすることができるのです。上記式では例えが作り

にくいので、

　

　

　

　

と使用する式を単純化しますね　(^-^)/

前回に引き続きサンプルファイルを使用しますのでダウンロードして確認してみて

ください。

　

　

　

サンプルファイル　：　Sankaku

　

　

　

今回変化させる変数は、前回のNに加えてAの値も変化させます。まず下記条件に

てSin波・Cos波の合成波を作成してみます。

　　

　

ⅰ）　N＝１～１０とします

ⅱ）　Sin・Cos共にN=１のAを５とする

　

　

　

■　N=１のAを５としてN=１～１０までのSin波による合成波

　

　

　

N=1単体のSin波の波形がデコボコになったような波形が作られましたね　(^O^)/

　

　

　

　

■　N=１のAを５としてN=１～１０までのCos波による合成波

　

　

　

これまたN=１のCos波がデコボコになったかのような波形です。

　

　

　

　

■　上図Cos・Sin波の合成波

　

　

　

ここまで波形が複雑になると価格変動っぽい感じもしてきますよねえ。ということ

でパラメータであるAの値を変化させることでも波形は変化するのでした　('-^*)/

最後にN毎のAを適当に設定した波形も載せておきましょうか。

　　

　

　

　

相当に複雑になりましたね　(;^_^A
　

　

　

　

　

　

　

【改めてフーリエ級数】
ここまでに互いにパラメータが異なるSin波・Cos波の合成波が相当に複雑な

波形になることがわかりました。ではフーリエ級数ってのは何を意味している

のでしょう？

　

　

　

　

実は、今までの例題を用いればフーリエ級数の仕組みってのは簡単に理解で

きると思います。

まず、N＝１～１０とした例題では、Σの式の　ｎ　が１～１０　であることを意味し

ます。そしてN＝１～１０の合成波が　Σ　によって表現されているのですねえ。
ただ、例題では　an　bn　に相当する「パラメータA」を適当に設定しましたが、

フーリエ級数では係数は公式化されていましたよね？

　　

　

　

　

　

これは、観測対象のデータである　ｆ（ｘ）　に対して　ｎ次　までの三角関数、

（今回扱った例ではN＝１～１０なので１０次）を乗算して－π～π区間で積分

すれば係数が求まりますよということなのです。要は、

　

　

・　フーリエ級数は三角関数をもって観測対象のデータに近似させる

・　ただし、係数は観測対象のデータとN次における三角関数との乗算の積分で求める

　

　

ということなのです。なんで観測対象のデータである　ｆ（ｘ）と三角関数の乗算

の－π～π区間における積分で係数が求まるの？と思われた方は本格的に

勉強してみる価値があります。これを解説するには関数の直交性の詳細をし

ないといけないので省略します。最低限知っておきたいことは、

　

　

フーリエ級数は互いに異なるパラメータである三角関数の合成波

を観測対象のデータに近似するようにしたもの

　

　

ということです。そして、複素フーリエ級数ってのはフーリエ級数の計算を求め

やすくするためにしたものと理解しておきましょう。複素フーリエ級数は難しい

と思われてしまいますがフーリエ級数からの発展版に過ぎません。どちらも中

身は同じなので後は計算プロセスをフーリエ級数でのプロセスをイメージして

おけばOKということなのです　(^-^)/